T(n) = n × (n + 2) × (2n + 1) ÷ 8
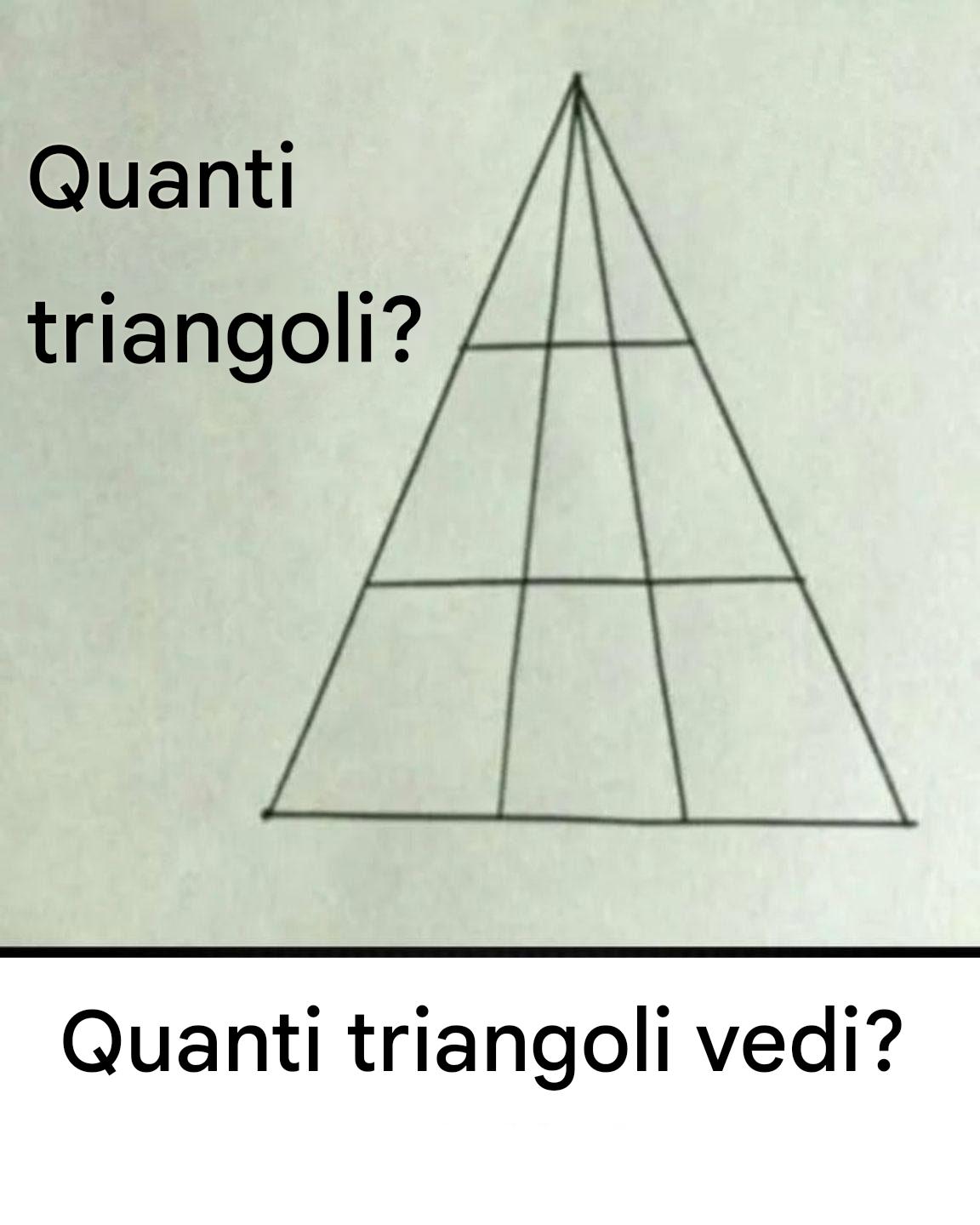
Applicato a n = 4:
T = 4 × 6 × 9 ÷ 8 = 27
Questo risultato corrisponde perfettamente al nostro conteggio passo dopo passo. Il bello di questa formula è che « conta » tutte le dimensioni possibili, comprese le combinazioni multilivello. Ideale per mettere alla prova il tuo intuito… o per mettere a tacere un acceso dibattito!
Errori comuni (e come evitarli)
- Contare “per livelli” senza controllare i grandi triangoli a croce: il colpevole tipico è un triangolo a 3 livelli dimenticato.
- Omettiamo i triangoli invertiti (“verso il basso”): sono meno visibili, ma comunque presenti (7 in totale).
- Aggiungi linee verticali immaginarie: alcune varianti del puzzle includono linee verticali reali, che modificano il totale (ma mai a 26). Assicurati di aver impostato correttamente la posizione prima di concludere.
- Raddoppiare alcuni triangoli: seguire una progressione logica in base alle dimensioni per evitare duplicati.
Vuoi approfondire?
- Cambia il numero di righe: prova la formula con n = 3 o n = 5 e confrontala con un conteggio manuale: perfetto per allenare l’occhio.
- Cronometrati: concediti 60 secondi per raggiungere 27. Il segreto? Conta prima la parte « in su », poi aggiungi quella « in giù ».
- Spiegalo a un amico: insegnare un trucco significa ricordarlo per sempre (e vincere la tua prossima battaglia di enigmi).
Perché dietro un semplice triangolo si nasconde spesso una piccola lezione di logica… e il discreto piacere di avere l’ultima parola